- Course overview
- Search within this course
- Network analysis in biology
- Types of biological networks
- The sources of data underlying biological networks
- Protein-protein interaction networks
- Building and analysing PPINs
- Summary
- Quiz: Check your learning
- Your feedback
- Learn more
- References
Graph theory: network topology
Graphs have some properties that are very useful when unravelling the information that they contain. It is important to realise that the purpose of any type of network analysis is to work with the complexity of the network to extract meaningful information that you would not have if the individual components were examined separately.
Network properties, and particularly topological properties, can help us identify relevant sub-structures within a network.
Topology is the way in which the nodes and edges are arranged within a network. Topological properties can apply to the network as a whole or to individual nodes and edges. Some of the most used topological properties and concepts are:
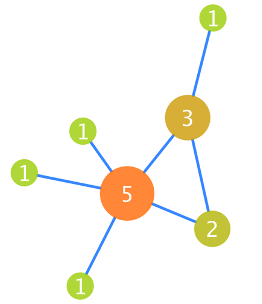
- The degree of a network – The degree is the number of edges that connect to a node. It is a fundamental parameter that influences other characteristics, such as the centrality of a node. The degree distribution of all nodes in the network helps define whether a network is scale-free or not, as we will see later. In the figure, the degree of each node is indicated and reflected in its size and colour (Figure 5). Directed network nodes have two values for degree: out-degree for those edges coming out of the node and in-degree for those edges coming into the node.
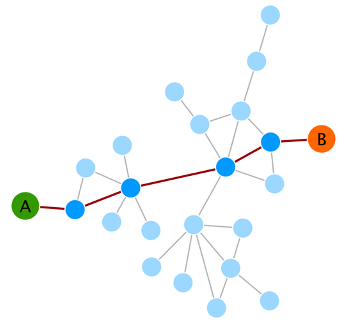
- Shortest paths – Shortest paths, or the shortest distance between any two nodes, is used to model how information flows. This is especially relevant in many biological networks. In the figure, the shortest path between nodes A and B is highlighted and takes five steps (Figure 6).
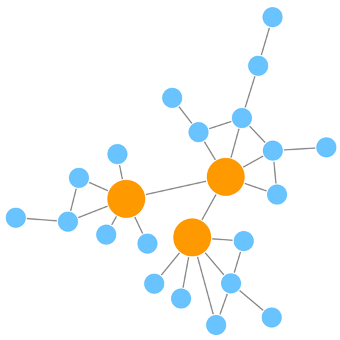
- Scale-free networks – In scale-free networks most of the nodes are connected to a low number of neighbours and there are a small number of high-degree nodes (hubs) that provide high connectivity to the network. In the figure, hubs are highlighted in orange (Figure 7).
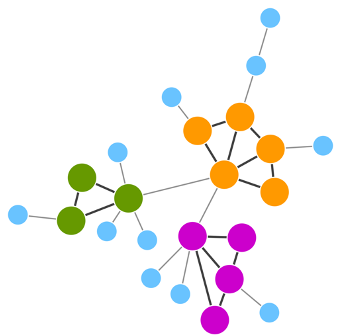
- Transitivity – Transitivity relates to the presence of tightly interconnected nodes in the network called clusters or communities. These are groups of nodes that are more internally connected than they are with the rest of the network. These groups are also called topological clusters and are highlighted in the figure (Figure 8).
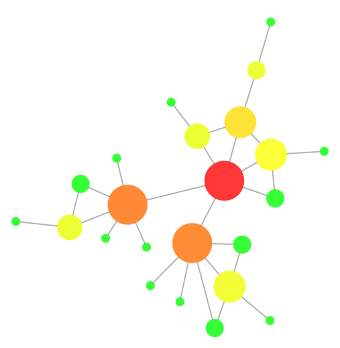
- Centralities – As we will see later, there are different flavours of centrality, each representing different concepts. Centrality can be measured for nodes and for edges and gives an estimation on how important that node/edge is for the connectivity or the information flow of the network. The degree of a node has a direct influence on many centrality measures, most prominently on the ‘degree centrality’. Its significance is reduced in more sophisticated types of centrality measures, for example, betweenness centrality. In the figure, the most central nodes (according to their betweenness centrality) are highlighted in warm colours and the node size reflects its degree (Figure 9).