Betweenness centrality
Betweenness centrality is based on communication flow. Nodes with a high betweenness centrality are interesting because they lie on communication paths and can control information flow. These nodes can represent important proteins in signalling pathways and can form targets for drug discovery. By combining this data with interference analysis we can simulate targeted attacks on protein-protein interaction networks and predict which proteins are better drug candidates, for example see Yu, et al 2007 (15).
The calculation of betweenness centrality is not standardised and there are many ways solve it. It is basically defined as the number of shortest paths in the graph that pass through the node divided by the total number of shortest paths.
Betweenness centrality measures how often a node occurs on all shortest paths between two nodes. Hence, the betweenness of a node N is calculated considering couples of nodes (v1, v2) and counting the number of shortest paths linking those two nodes, which pass through node N. Next the value is related to the total number of shortest paths linking v1 and v2.
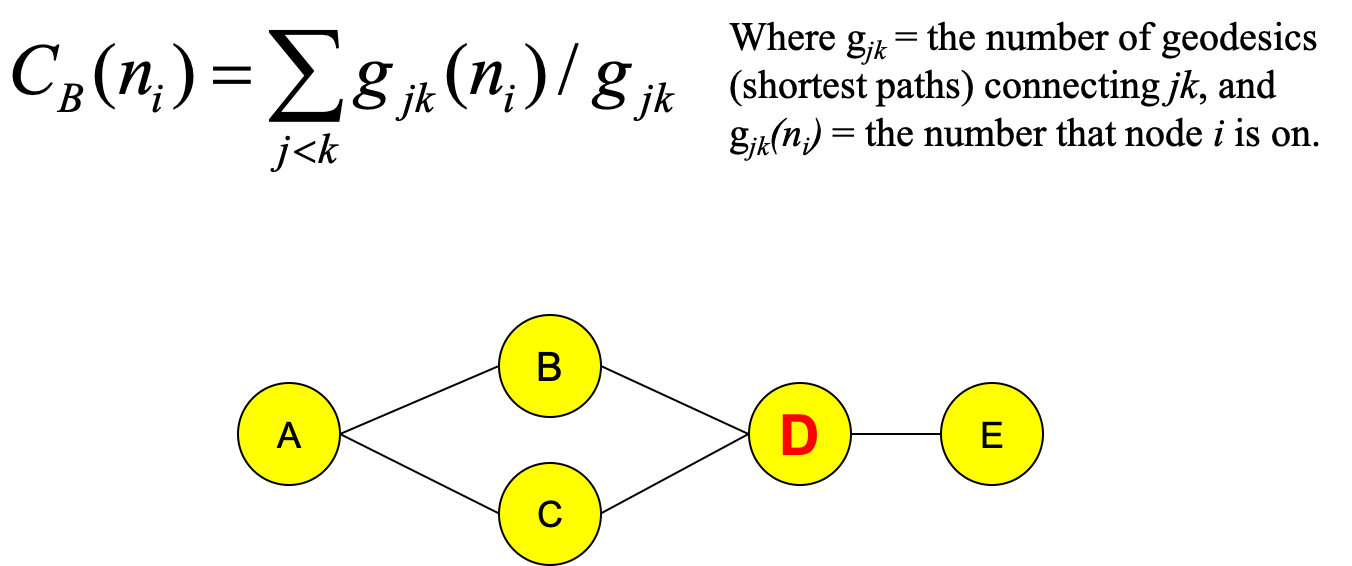
To give a more intuitive example, in the graph from Figure 29, either node B or node C can be removed and there will still be paths leading to node E. Node D, however, is quite central, since it is required for any path leading to node E. You can think of this graph as a city map and our analysis is telling us that D is the cross roads where traffic jams are more likely to occur. Betweenness centrality can in fact be used in city planning and there are studies aiming to optimise city transport based on this and related metrics (16).